董世平／中原大學應用數學系教授，美國伊利諾大學數學博士，專長數理邏輯，曾任符號邏輯協會東亞委員會委員九年。
布爾追尋真理的熱忱，導引他發現思想的法則。他以代數的手法將思想法則表現為後人所稱的布爾代數，不僅成為電腦硬體設計的基礎理論，更開創了數理邏輯學的深刻發展。
天上的星星，依照牛頓所發現的「萬有引力定律」而運動；而人的思想，也有它運作的法則嗎？1854年，布爾出版了他的著作《思想法則之探討》，在這本書中，布爾給了上述問題的答案：人的思想是有法則可循的。不僅如此，我們可用數學的方式來描述這些法則。這本書出版之時，能明瞭的人甚少，但這本書對人類影響之大，絕對是當時的人，甚至布爾本人都難以想像的。
理性是人行事的基礎，如巴斯卡（Blaise Pascal, 1623~1662）所說：「人是會思考的蘆葦。」我們也說：「物有本末，事有先後。知所先後，則近道矣。」雖然人人做事都有其背後的邏輯，但意識到邏輯本身，應是後來的事，正如人人都呼吸，但意識到呼吸，乃至知道空氣的存在，都是相當後來的事了。一個人沒學過邏輯，甚至沒聽過邏輯，並不表示這人做事沒有邏輯，或不需要邏輯。
巴斯卡。 Source: shutterstock
邏輯學門的發展
亞里士多德（左）與他的學生亞歷山大。Source: shutterstock
一般來說，把邏輯或理則學當作一門系統知識來學習，是從亞里士多德開始，故傳統邏輯被稱為亞里士多德邏輯，大家最熟悉的即所謂的「三段論」。
大前提：人會死
小前提：蘇格拉底是人
結論：蘇格拉底會死
當我們從所知或已知的事物而得到結論時，這個思考或邏輯過程，皆使用三段論。人會犯錯，也會犯邏輯的錯誤，有可能是前提錯，即他的認知就是錯的，但也常發生的是，推論的過程產生錯誤：
大前提：人會死
小前提：蘇格拉底死了
結論：蘇格拉底是人
我們也許會說這種錯誤太不應該了，但犯這種錯誤的人比比皆是，在報章雜誌及電視上不時可見這些錯誤的推論。因這些人的心態是先有結論，再為結論找理由，也難怪會犯這種錯誤。希望我們能如孟子所說：「淫辭知其所陷」，而不為其所陷。邏輯在希臘哲學時期的建立，也就是為了分辨辯士在辯論時，何者是講理，何者是狡辯，進而使個人能合理的思考，正確的判斷。
邏輯不僅在希臘發展，在同時期的中國亦現其蹤跡。春秋戰國時期的名家及墨家的論述中也都有「邏輯詭論」，或如莊子所說：「一尺之杖，日取其半，萬世不竭。」；在希臘有完全相同的說法，如「飛矢不動」，也與「阿基里斯詭論」有相通之處。但可惜的是，中國的邏輯後來未有系統性的發展，僅留下了「矛盾」這個有趣的典故：楚人有鬻盾與矛者，譽之曰：「吾盾之堅，物莫能陷之。」以譽其矛曰：「吾矛之利，於物無不陷也。」或曰：「以子之矛陷子之盾，何如？」其人弗能應也。夫不可陷之盾與無不陷之矛，不可同世而立。」─《韓非子》。
邏輯數學化
人類用亞里士多德的方式學習邏輯，至今已2500 年了。然而，我們必須用「理性」，才能得到邏輯正確的結果嗎？唯有「理性」，才能知道「理」之「則」嗎？
布爾提出兩個突破性觀念：其一，用符號表示邏輯命題；其二，可用代數作符號運算。總體來說，我們可先用符號代表命題，用公理表示邏輯的規則，再以代數的方式運算。在運算的過程中，不需考慮符號本身及運算的意義，運算完畢，將符號再帶回原本的命題，即為邏輯正確的結果。至此，推論的過程完全被公式的運算取代，不僅大大增加處理命題的能力，完全避免人有意無意的錯誤，藉著公理的選擇，可發現命題之間的關聯，亦可清楚看見邏輯的本質，其好處不勝枚舉，更有許多後世才發現的益處。
布爾在他著作中未曾提出一套完整的公理系統，也因此現今我們有許多種不同的布爾代數系統，本文僅列出一個較簡潔的系統，我們藉此來討論布爾將邏輯符號化及代數化的意義。
在討論符號化的意義之前，我們先引用布爾在他1847年所出版《邏輯之數學分析》中所說的：「認識現今符號代數情形的人都明瞭，分析過程的正確性並非建立在對符號所用的解釋，而是在它們組合的定律上。」使用符號不僅為方便表示，亦使我們不再受限於特定的解釋，因此可擴展應用的範圍，也才有現今各樣的數位產品。
我們藉由布爾曾用的交換律b+a=a+b 來說明。你可把a、b視為兩個集合，+為聯集，=為集合相同；亦可把a、b視為整數，+為加法，=為數字相等；亦可把a、b視為命題，+視為邏輯連辭「或」，而=視為意義相等。在應用時我們固然需要對這些符號賦予特定的意義，但在推導性質時，我們只需按著他們組合的定律來做，如交換律，如此所得的性質可用在集合、數字或命題及其他可能的解釋上。
對於邏輯的數學化，我們可用布爾所用的另一個例子來說明：
x2 = x → x－x2 = 0 → x(1－x)=0
這個過程相信是任何學過解方程式的人都明白的，當把0視為空集合，1視為包含所有個體的宇集（universalclass），1－x為包含所有不在集合x內個體的集合，x2=x 則意義為「具性質P 且具性質P 的集合，即為具性質P的集合」，因此布爾用上述的代數過程得到了古典邏輯中集合的「矛盾原則」，即不可能有一個集合同時具有性質P及性質非P，亞里士多德視矛盾原則為邏輯的基礎公理，但布爾則用數學方法顯示矛盾原則可由另一個看來更直觀的x2=x 公理所導出。
邏輯的符號化及數學化並非始自布爾，有不少的先驅者，最著名的當是萊布尼茲（Gottfried Wilhelm Leibniz,1646~1716），較布爾早生了約170 年。萊布尼茲曾期望當兩個人辯論時，兩個人能坐下來說：「我們算一算。」也就是用數學方法來解決爭論。符號化及數學化的威力已為現今所認知，但這兩者也意謂著抽象化，離人的直觀與經驗越來越遠。這似乎為認識事物本質所必要的，我們亦見此於物理的發展。由布爾的成就我們亦可見，透過抽象化，我們可更清楚認識及了解「思想」這個原本極為抽象的概念。
萊布尼茲。Source: shutterstock
范氏圖與真值表
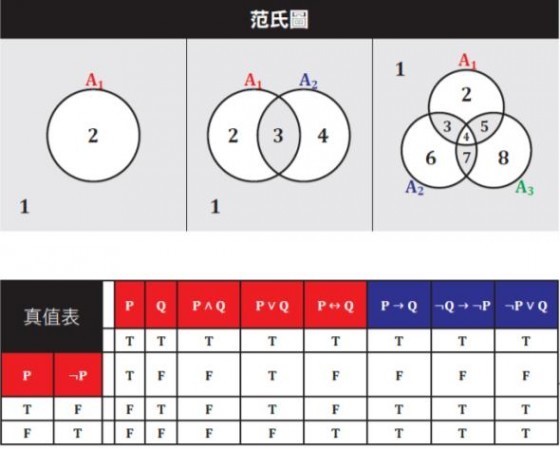
邏輯在布爾之後有極迅速的發展，現今常用兩種工具：范氏圖及真值表。由前列布爾代數公理，我們可見「集合代數」是一個布爾代數。史東（Marshall H. Stone, 1903~1989）亦證明了任一布爾代數可用一「集合代數」表示。范氏圖即為我們常用來表示集合關係的一個視覺化工具，而視覺化表示亦為布爾使用符號所希望能達到的目標，使人有更直觀的認知，但使用視覺化工具須注意其侷限性。
范氏圖用圓表示集合，1、2、3個圓交疊後，分別可得2、4、8個區域，每一個區域代表每一個集合僅使用一次可得交集的情形，在3個圓交疊的情形下，區域2為，區域為。那4 個圓交疊可得幾個區域呢？我們也許會猜21=2、22=4、23=8、24=16，16個區域，但我們若認真的去畫，我們會發現最多只能畫出14個區域。
然而，4個集合實際上應該有16個區域，所以范氏圖無法表示n ≥ 4個集合所有可能的情形，用n個圓最多可畫出多少個不同的區域？這個例子告訴我們，用歸納法一開始所得的歸納結果有可能是錯的，有興趣的讀者可嘗試用歸納法得到正確的公式，再用數學歸納法證明公式是正確的。
另一個有用的工具則是真值表。它用P、Q代表命題，∧（且）、∨（或）、¬（非）、→（若⋯，則）、→（若且唯若）、T（真）、F（假），我們有下列定義：
我們可看見P → Q 和¬Q → ¬P 及¬P ∨ Q 對應的真假值完全一樣，即此三者為邏輯等價，當我們要證明「若P則Q」（P→ Q） 時， 我們證明「若Q為假，則P為假」（¬Q → ¬P），則「若P 則Q」得證，此即為「歸謬證法」或「矛盾證法」的本質，同理，若我們能證¬P ∨ Q 為真，我們亦證明了「若P 則Q」。
布爾之後的邏輯
邏輯非自布爾而始，亦非自布爾而終，但邏輯自布爾後，就再也不一樣了。我們也許可以如此比擬：克卜勒藉著對行星運動的觀察數據，以計算及歸納得到了「克卜勒行星運動定律」。牛頓依此發現了「萬有引力定律」，如此不僅可解釋「克卜勒行星運動定律」，我們亦可藉此定律計算出物體的運動軌跡。同樣的，亞里士多德歸納出正確思想應該遵守的規則，而布爾用代數的方法解釋了正確思想的規則，我們便可藉著他的發現，計算出正確思想應得的結論。
布爾的觀念及符號就留在現今數學裡，因為他使用符號的方式來處理邏輯，我們也就有了「符號邏輯」這個名詞。現今邏輯界最重要的學會，即「符號邏輯協會」（The Association for Symbolic Logic），而它所出版的代表期刊即名為《符號邏輯期刊》（The Journal of Symbolic Logic）。當代對邏輯的研究主要來自數學、哲學與計算機領域，對布爾代數本身的研究亦極活躍，蒙克（Donald Monk）主編了共三冊的《布爾代數手冊》（Handbook of Boolean Algebras），從其中包含的多樣主題，即可見布爾在數學的影響之廣。
現今一些較熱門的題目也和布爾邏輯有所關聯，例如，哲學界所研究的「非古典邏輯」，其研究的方式多為先將布爾代數用不同的公理表示，再將其中一些公理，基於哲學方面的考量加以弱化，如此可得如直觀邏輯（Intuitive Logic），模態邏輯（Modal Logic）等等不同的邏輯。
人工智慧
人工智慧則是一個常被討論的題目：機器能有智慧嗎？布爾告訴我們，機器藉由代數推導後，可得到正確的結論。在命題邏輯不考慮計算複雜度（computational complexity）的前提下，人所能做到的，機器都可做到。但在一階邏輯時，筆者認為由「哥德爾不完備定理」可知，機器所能做的無法跟人一樣，這也是潘洛斯（Roger Penrose）在《皇帝新腦》（Emperor’s New Mind）書中所用的論證，這仍是人工智慧學者一個爭論不休的問題。
乏晰邏輯
乏晰邏輯（Fuzzy Logic）在工業界已有許多的應用，其特點是，一個命題的真假值可為一個介於0 與1 之間的實數p，亦可視為[0, p] 區間；而傳統邏輯下，一個命題的真假值限定為假與真，或布爾所用的0 與1 表示。
1960 年代， 邏輯學者逐漸發展出布爾值模型（booleanvalued model），其命題的真假值對應至一個布爾代數，並以此將柯亨（Paul J. Cohen, 1934~2007）的結果( 註) 給予一個相對簡潔的證明。此處須特別強調「無法證明是對的」和「錯的」其意義是不相同的。由布爾值模型後，又發展出布爾值分析（boolean-valued analysis），並由此得到數學上有意義的成果，乏晰邏輯可說是布爾值模型另一個有用的特例。
註：此結果得到數學最大獎菲爾茲獎，其敘述在使用一般通用的集合論公設時，無法證明選擇公設（Axiom of Choice）和連續統假說（Continuum Hypothesis）是對的。
量子邏輯
另一個著名的非古典邏輯為「量子邏輯」，由量子邏輯可衍伸出「量子計算機」。其使用量子演算法，可在多項式時間內做「因數分解」，這是一般計算機與圖靈機（Turing machine）至今仍無法得到的結果。但量子計算機與圖靈機所能計算的函數總體是相同的，量子計算機與現今使用的計算機相較，或許其計算複雜度有差別，但從可計算性（computability）來看，兩者並無不同。
英國科學家潘洛斯，在物理、數學等領域有卓越貢獻。他曾撰寫過一系列探討人類意識與物理之間關係的書籍，如1989 年出版的《皇帝新腦》。Source: Festival della Scienza
綜合上述，我們可說現今邏輯與計算的發展，都是建立在布爾的基礎上，我們是沿著他給我們的方向繼續前進，而他的影響不僅遍及數學各領域，亦延伸至其他領域，如哲學、計算機科學、語言學等。
對真理的追求
我們不禁要問：為什麼布爾能有如此偉大的成就？當然他一定是個天才，但他的成就並非憑空而來，他也經過時間的醞釀，使他的思想日漸成熟。也由於這些成就，使他對符號的能力有更清楚的認識。他先前出版的《邏輯之數學分析》不僅不成熟也包含謬誤。在思考的過程中，他也曾面對失敗與挫折，但他不放棄，因此得以出版《思想法則之探討》。另外他勇氣過人，他敢思想「思想」，這個極端抽象卻又最根本的問題，大名鼎鼎的萊布尼茲嘗試過、努力過，但無特別的成果，而布爾不畏艱難，終於有所成。
最後，因布爾具有「對真理追求的真誠」（It is integrity in pursuit of the truth），在他寫給好友笛摩根的信中，他先說笛摩根具有這個特質，而他在這一點並不會輸給笛摩根，他甚至寫了下面的話：「我不認為任何人比我寫那本書時的心智，曾充滿更熱烈的渴望，僅為了要發現並說出真理，而不為其他。（I don’t think any man’s mind ever was imbued with a more earnest desire to find out the truth and say it and nothing else, than mine was while writing that book.）」就是這種真誠讓布爾發現了「思想」的法則，這個發現也改變了人類。
本文選自《科學月刊》2015年11月號
延伸閱讀：
喬治．布爾─自學成大器的數學家
布爾與電腦
什麼？！你還不知道《科學月刊》，我們46歲囉！
入不惑之年還是可以當個科青
The post 布爾與邏輯－－《科學月刊》 appeared first on PanSci 泛科學.